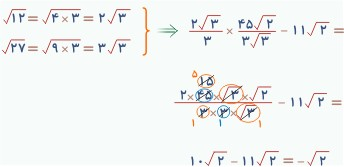
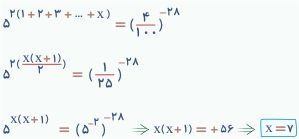. معادله نسبیت عام
معادله
بالا بخشی از توصیف نظریه نسبیت عام توسط آلبرت اینیشتین در سال 1915
میلادی است. این نظریه انقلابی را ایجاد کرد که سبب شد دنیای علم را با
نحوه ارتباط مشخصه هندسی کائنات با فضا و زمان توضیح بدهد!
ماریو
لیویو منجم و ستاره شناس و اختر فیزیکدان برجسته موسسه علوم تلسکوپی در
آمریکا بیان می کند: «قسمت سمت راست معادله انرژی کائنات را نشان می دهد
(شامل انرژی ماده تاریک که نقش بسزایی در تعیین سرعت کهکشان ها دارد) و سمت
چپ معادله بعد هندسی فضا-زمان را توصیف می کند. این معادله اینشتین ثابت
می کند که جرم و ماده هندسه فضا را مشخص می کند و در نهایت چیزی را آشکار
می سازد که ما آن را جاذبه می نامیم!»
کایل کرانمر فیزیکدان دانشگاه
نیویورک نیز می گوید: «با استفاده از این رابطه چرخش اجرام به دور اجرام
سنگین تر و همچنین بسیاری دیگر از پدیده های نجومی و فیزیکی نظیر سیاهچاله
ها را می توان اثبات نمود».
2. مدل استاندارد
یکی
دیگر از معادلات بسیار مهم و بنیادی فیزیک معادله مدل استاندارد است که
توصیف ذرات بنیادی جهان حاضر است. این معادله بر گرفته از یک معادله کلی تر
به نام معادله استاندارد لاگرانژ (ریاضیدان و ستاره شناس قرن 18 فرانسه)
است. لنس دیکسون متخصص برجسته شتاب دهنده کالیفرنیا می گوید: «این معادله
به صورت موفقیت آمیزی تمامی ذرات بنیادین که تا کنون کشف شده اند نظیر ذره
هیگز را بیان می کند اما تاکنون این معادله موفق نشده است که گرانش را
توصیف نماید».
معادله نسبیت خاص انیشتین بیان می دارد که مفاهیم فضا و زمان مفاهیمی مطلق نیستند بلکه به سرعت بیننده وابسته هستند
3. قضیه اساسی حساب
در
حالی که 2 معادله پیشین در مورد ذرات تشکیل دهنده هستی بوده است اما
معادله حساب ستون فقرات ریاضیات محسوب می شود که در خلاصه این محاسبات در 2
مفهوم انتگرال گیری و مشتق گیری خلاصه می گردد.
قضیه اساسی حساب در
قرن های اولیه بشریت نیز وجود داشته و پایه ریزی شده است اما در قرن 17
توسط نیوتن گسترش داده شد. وی از این قضیه برای توصیف حرکت سیارات به دور
خورشید استفاده می کرده است.
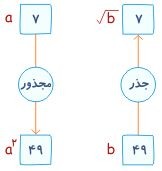
4. قضیه فیثاغورث
معادله
«اودی یا گودی» که به قضیه فیثاغورث مشهور است. این قضیه می گوید که در
مثلث قائم الزاویه مجذور وتر برابر است با مجموع مجذور اضلاع مجاور وتر!
داینا
تایمینا از دانشگاه کرنل می گوید که: این قضیه جزء اولین روابطی بود که من
را بسیار شگفت زده کرد که چگونه می توان هندسه را با روابط ریاضیاتی ترکیب
نمود!»
5. معادله اویلر
این معادله به ظاهر ساده حقایق بسیار زیبایی را در مورد کره ها بیان می کند.
کالین
آدامز از کالج ویلیامز در ایالت ماساچوست می گوید: «این معادله بیان می
دارد که اگر شما سطح یک کره را به یک چندوجهی تبدیل کنید به طوری کهF
بیانگر تعداد وجه ها و E بیانگر تعداد لبه ها و V بیانگر تعداد رئوس باشد
آنگاه همواره این معادله برقرار است: V-E+F=2
این رابطه برای هر نوع
چندوجهی برقرار می باشد مانند هرم های 8 وجهی و غیره. حقیقت جالب این است
که این معادله می تواند به ما اطلاعاتی در مورد ساختار اولیه کره ها قرار
بدهد».
6.نسبیت خاص
معادله
نسبیت خاص انیشتین بیان می دارد که مفاهیم فضا و زمان مفاهیمی مطلق نیستند
بلکه به سرعت بیننده وابسته هستند. معادله بالا نشان می دهد که چگونه کاهش
زمان یک رویداد با سرعت بیننده وابسته می باشد. بیل مورای از محققان
برجسته شتاب دهنده سرن در ژنو می گوید: «برای یک دانشجوی قوی حل یک معادله
سخت ریاضی و یا انتگرال های پیشرفته مهم نیست بلکه چیزی که مهم است نحوه
نگاه کردن به پدیده های مختلف فیزیکی و ریاضیاتی و درک مفاهیم آن است و
بتواند این مفاهیم را با جهان خارج ارتباط داد».
7. 0.99999999 = 1
این
معادله نماد این است که مقادیر مطلق در جهان وجود ندارد. این مطلق نبودن
خود را در ساده ترین شکل و پایه ترین عدد یعنی 1 نشان می دهد که 1 برابر
است با حد بینهایت 9 و مقدار مطلق 1 وجود ندارد!
8.معادله اویلر لاگرانژ و قضیه نوتر
کرانمر
از دانشگاه نیویورک می گوید: «این معادله هر چند خلاصه است اما مسایل
بسیاری را نشان می دهد. این معادله انقلاب بزرگی را در مکانیک کوانتومی
ایجاد کرده است.
L در این معادله که اول کلمه لاگرانژ است پارامتری است که برای اندازه گیری انرژی سیستم به کار می رود.
قضیه
دیگری نیز در رابطه با این رابطه وجود دارد به نام قضیه نوتر که می گوید
اگر شما در سیستم خود تقارن داشته باشید امکان ذخیره سازی انرژی بهتر وجود
خواهد داشت. از این قانون در طراحی های مکانیکی و فضاپیماها استفاده می
شود».
9.معادله کالان-سیمانزیک
معادله
کالان سیمانزیک یک معادله بسیار حیاتی در فیزیک کوانتوم است. مت استراسلر
فیزیکدان نظری دانشگاه راتجرس می گوید: «این معادله نشان می دهد که
انتظارات ساده چقدر راحت در دنیای کوانتوم به شکست می انجامد! این معادله
به فیزیکدانان بسیار کمک می کند که بتوانند اندازه جرم های کوانتومی نظیر
پروتون و اندازه هسته را مشخص بکنند. معادله کالان سیمانزیک می تواند به ما
نشان بدهد که نیروی گرانشی و الکتریکی بین 2 ماده با معکوس مجذور فاصله
بین آن 2 متناسب می باشد.
این معادله روابط بسیار پیچیده بین ذرات
تشکیل دهنده نوترون ها و پروتون ها (کوارک ها) و نحوه نزدیک ماندن آنها با
یکدیگر و در نتیجه تشکیل هسته را به ما توضیح می دهد. این معادله کاربردی
بیشتر در ابعاد کوچکتر از پروتون و نوترون به کار می رود و می تواند اثرات
ذرات در این ابعاد را برای محققان توصیف نماید».
10. معادله سطح حداقل
فرانک
مرگان از کالج ویلیامز می گوید: «این یک معادله غیر خطی است برای همین این
معادله با معادلات خطی مشتقات جزیی مشهور نظیر معادلات گرما و معادله صوت و
معادله شرودینگر در فیزیک کوانتوم در تضاد می باشد».
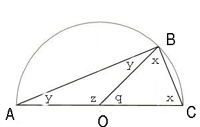
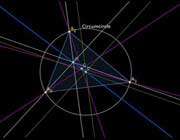
11. خط اویلر
گلن
ویتنی بنیانگذار موزه ریاضیات در نیویورک می گوید: «معادله ای که نام آن
به نام کاشف آن لئونارد اویلر فیزیکدان و ریاضیدان قرن 18 سوییس نام گرفت
بیان می دارد که اگر شما در هر مثلثی نقطه مرکز ثقل (نقطه ای که اگر شکل را
بر روی یک سوزن قرار بدهیم آنگاه شکل به حال تعادل قرار می گیرد) و نقطه
محل برخورد ارتفاع های هر یک از اضلاع و همچنین مرکز دایره محاطی مثلث را
مشخص نمایید، همواره این 3 نقطه در حالت های مختلف بر روی یک خط به نام خط
اویلر قرار دارد. این قضیه شگفتی ریاضیات را در توصیف الگوهای شگفت آور در
اشکال ساده نمایش می دهد».
منبع:http://www.tebyan.net/newindex.aspx?pid=270976



[ بازدید : 237 ] [ امتیاز : 3 ] [ نظر شما :
]
![]()



















 نشان دهنده میزان تغییرات یک کمیت است. ولی در حال حاضر برای محاسبه مشتق توابع،بیشتر از فرمول زیر استفاده میکنند:
نشان دهنده میزان تغییرات یک کمیت است. ولی در حال حاضر برای محاسبه مشتق توابع،بیشتر از فرمول زیر استفاده میکنند:





 و
و  حاصل میشود.واضح است که در این روش فقط یک نقطه روی خط برای ما معلوم است
و نیازی برای بدست آوردن نقطه دوم روی خط وجود ندارد.همچنین در این روش
مشتق x ،حاصل حد زیر است:
حاصل میشود.واضح است که در این روش فقط یک نقطه روی خط برای ما معلوم است
و نیازی برای بدست آوردن نقطه دوم روی خط وجود ندارد.همچنین در این روش
مشتق x ،حاصل حد زیر است:
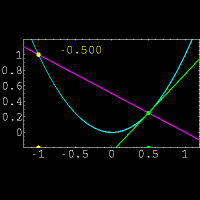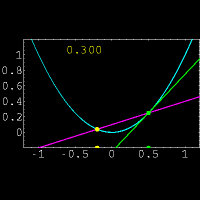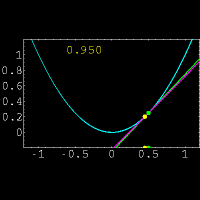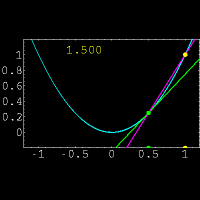
 یک نقطه بحرانی در x=0 دارد، ولی میتوان از نمودار تابع متوجه این نکته شد که تابع در این نقطه دارای ماکزیمم یا مینیمم نسبی نیست.
یک نقطه بحرانی در x=0 دارد، ولی میتوان از نمودار تابع متوجه این نکته شد که تابع در این نقطه دارای ماکزیمم یا مینیمم نسبی نیست.




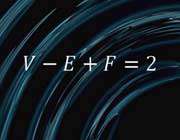



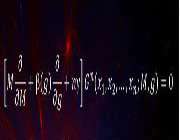




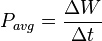
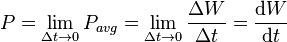


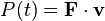

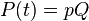
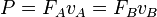




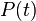 توان لحظهای است به وات.
توان لحظهای است به وات. 

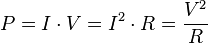


 با دورهی
با دورهی  ، مانند زنجیرهای از پالس های یکریخت، توان لحظهای
، مانند زنجیرهای از پالس های یکریخت، توان لحظهای 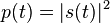 نیز تابعی متناوب با دوره
نیز تابعی متناوب با دوره ![P_0 = max [p(t)]](http://upload.wikimedia.org/math/a/b/5/ab5143f0ee5b1e4c6c19d0479061dbb1.png) تعریف میشود. توان اوج همیشه به سادگی قابل اندازهگیری نیست، اما
اندازهگیری توان متوسط معمول تر است. اگر انرژیِ هر پالس را به صورت زیر
تعریف کنیم:
تعریف میشود. توان اوج همیشه به سادگی قابل اندازهگیری نیست، اما
اندازهگیری توان متوسط معمول تر است. اگر انرژیِ هر پالس را به صورت زیر
تعریف کنیم:

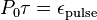 تا نسبت زیر برقرار باشد. به این نسبت چرخهی کار زنجیره پالس ها میگویند.
تا نسبت زیر برقرار باشد. به این نسبت چرخهی کار زنجیره پالس ها میگویند.