مستطیل ها ی محاطی و مستطیل های محیطی و مجموع پایین ریمان و مجموع بالای ریمان
[ بازدید : 506 ] [ امتیاز : 4 ] [ نظر شما : ]
[ دوشنبه 3 فروردين 1394 ] 22:01 ] [ امیرحسین جعفری ]
[ ]
ریاضی خونهریاضی علم شیرین
|
مستطیل ها ی محاطی و مستطیل های محیطی و مجموع پایین ریمان و مجموع بالای ریمانhttp://0up.ir/do.php?filename=int1.rar [ بازدید : 506 ] [ امتیاز : 4 ] [ نظر شما : ] [ دوشنبه 3 فروردين 1394 ] 22:01 ] [ امیرحسین جعفری ] [ ] ریاضی و ارطباط آن با علم و فناوری و جامعهhttp://0up.ir/do.php?filename=Nashr-e-Riyazi.pdf  [ بازدید : 229 ] [ امتیاز : 3 ] [ نظر شما : ] [ دوشنبه 3 فروردين 1394 ] 20:47 ] [ امیرحسین جعفری ] [ ] ضرب ماتریسهاضرب ماتریسهاضرب اسکالر در ماتریساگر و و یک اسکالر باشد، آنگاه یک اسکالر باشد، آنگاه
نکته: اگر  و و  دو اسکالر و دو اسکالر و  و و  دو ماتریس از مرتبه ی دو ماتریس از مرتبه ی  باشند، آنگاه: باشند، آنگاه:
    ضرب ماتریس در ماتریساگر و و  ، آنگاه ضرب دو ماتریس را با علامت " ، آنگاه ضرب دو ماتریس را با علامت " " نمایش داده و بصورت زیر تعریف خواهیم کرد: " نمایش داده و بصورت زیر تعریف خواهیم کرد:
 به عنوان مثال اگر  و و  دو ماتریس به قرار زیر باشند: دو ماتریس به قرار زیر باشند:
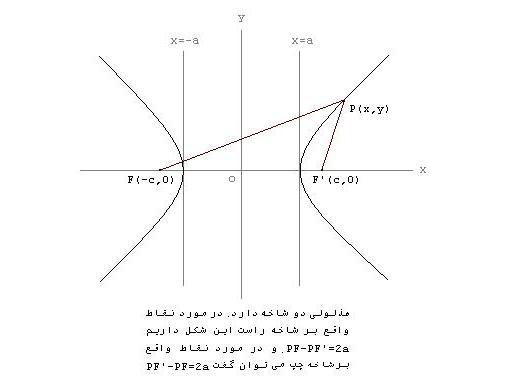 آنگاه: 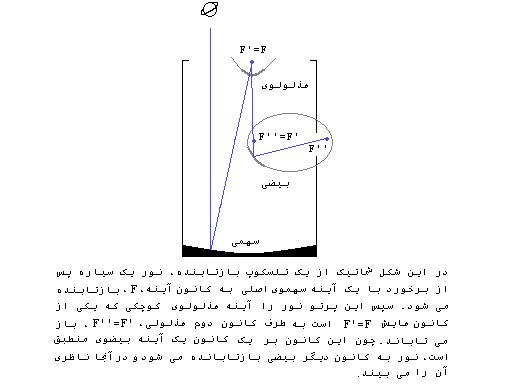 نکته:
خواص ضرب ماتریسها
منبع :رشد [ بازدید : 357 ] [ امتیاز : 3 ] [ نظر شما : ] [ دوشنبه 3 فروردين 1394 ] 21:51 ] [ امیرحسین جعفری ] [ ] دنبالهمفهوم دنبالهمجموعه اعداد زوج طبیعی را در نظر بگیرید اولین عضو این مجموعه عدد 2 است و n امین عضو آن 2n است. اولین عضو این مجموعه عدد 2 است و n امین عضو آن 2n است.
حال مجموعه اعداد طبیعی را در نظر بگیرید:  با کمی دقت متوجه میشویم که میتوان یک تابع یک به یک از مجموعه اعداد طبیعی
به مجموعه اعداد طبیعی زوج تعریف نمود که در عضو از مجموعه اعداد طبیعی را
به یک عضو از مجموعه اعداد طبیعی زوج متناظر کند.(مانند شکل) با کمی دقت متوجه میشویم که میتوان یک تابع یک به یک از مجموعه اعداد طبیعی
به مجموعه اعداد طبیعی زوج تعریف نمود که در عضو از مجموعه اعداد طبیعی را
به یک عضو از مجموعه اعداد طبیعی زوج متناظر کند.(مانند شکل)
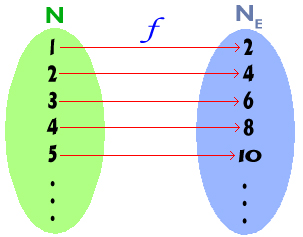 اگر این تناظر را به صورت مجموعه زوج های مرتب بنویسیم خواهیم داشت:  متوجه میشویم تابع
f از مجموعه اعداد طبیعی به مجموعه اعداد طبیعی زوج، تابعی است یک به یک
که هر عضو از دامنه خود را دو برابر میکند و به یک عضو از مجموعه اعداد
طبیعی زوج متناظر میکند و میتوان چنین ضابطهای برای آن تعیین نمود: متوجه میشویم تابع
f از مجموعه اعداد طبیعی به مجموعه اعداد طبیعی زوج، تابعی است یک به یک
که هر عضو از دامنه خود را دو برابر میکند و به یک عضو از مجموعه اعداد
طبیعی زوج متناظر میکند و میتوان چنین ضابطهای برای آن تعیین نمود: 
حال در مثالی دیگر تابع  را در نظر بگیرید. بیاید بجای اینکه به جای متغیر تابع عددی حقیقی قرار دهیم، متغیرهای طبیعی را جایگزین کنیم. در این صورت داریم: را در نظر بگیرید. بیاید بجای اینکه به جای متغیر تابع عددی حقیقی قرار دهیم، متغیرهای طبیعی را جایگزین کنیم. در این صورت داریم:
 مشاهده میکنید این تابع نیز هر عدد طبیعی را به عنوان ورودی دریافت میکند و آن را به یک عدد دیگر نسبت میدهد با این تفاوت که این تابع دیگر یک به یک نمیباشد و فقط بین اعداد طبیعی و مجموعه اعداد حقیقی یک تناظر بوجود میآورد. نمونه های دیگری نیز از این توابع وجود دارد مثلاً توابع  ، ،  ، که در آنها n عددی طبیعی است. ، که در آنها n عددی طبیعی است.
به چنین توابعی که از از مجموعه اعداد طبیعی به یک مجموعه دیگر تعریف میشوند دنباله میگوییم. در دنباله اعداد طبیعی زوج، عدد 2 از برد تابع را جمله اول، عدد 4 را جمله دوم و به همین ترتیب عدد 2n را جمله n ام دنباله میگوییم. همین شیوه برای سایر دنبالهها نیز اعمال میشود. در یک دنباله، اعداد طبیعی در دامنه به گونهای به اعضای برد متناظر میشوند که عدد طبیعی متناظر شده بیانگر شماره آن جمله در برد باشد به عنوان مثال در دنباله اعداد طبیعی زوج، عدد 1 در دامنه به عدد 2 در برد که اولین جمله دنباله است متناظر میشود و عدد 10 از دامنه به عدد 20 از برد که جمله دهم است متناظر میشود و به همین ترتیب عدد n در دامنه به عدد 2n از برد که جمله n ام است متناظر می شود. تعریف دنبالهدنباله (sequence) تابعی است که دامنه آن مجموعه اعداد طبیعی یا قطعه ای از مجموعه اعداد طبیعی باشد. پس در حالت کلی یک دنباله چون f تابعی است از مجموعه اعداد طبیعی به یک مجموعه دیگر چون A.  اگر دامنه دنباله قطعه ای از مجموعه اعداد طبیعی باشد دنباله را متناهی میگوییم و اگر دامنه دنباله خود مجموعه اعداد طبیعی باشد دنباله را نامتناهی میگوییم. به عنوان مثال دنباله اعداد طبیعی زوج کوچکتر از 10 یک دنباله متناهی است چرا که دامنه آن قطعه ای از مجموعه اعداد طبیعی یعنی  است و دنباله اعداد زوج دنبالهای نامتناهی است چرا که دامنه آن خود مجموعه اعداد طبیعی است. است و دنباله اعداد زوج دنبالهای نامتناهی است چرا که دامنه آن خود مجموعه اعداد طبیعی است.
برای مشخص کردن یک دنباله مانند هر تابع دیگر باشد دامنه و ضابطه آن را مشخص کرد. ضابطه یک دنباله را در اصطلاح جمله عمومی آن دنباله میگوییم. اگر f یک دنباله باشد جمله عمومی آن را با (f(n و یا به صورتی معمولتر به صورت 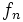 نشان میدهیم. پس برای نمایش مقدار دنباله f به ازای عدد طبیعی n بجای نماد (f(n معمولا از نماد نشان میدهیم. پس برای نمایش مقدار دنباله f به ازای عدد طبیعی n بجای نماد (f(n معمولا از نماد 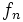 استفاده میکنیم. به عنوان مثال در دنباله اعداد طبیعی زوج داریم: استفاده میکنیم. به عنوان مثال در دنباله اعداد طبیعی زوج داریم: 
برای نمایش خود دنباله از نماد  استفاده میکنیم. پس دنباله اعداد طبیعی زوج را به این صورت نشان می دهیم: استفاده میکنیم. پس دنباله اعداد طبیعی زوج را به این صورت نشان می دهیم:
 دنباله حقیقیدنباله  را دنباله حقیقی میگویند هرگاه تابعی از مجموعه اعداد طبیعی به مجموعه اعداد حقیقی باشد به عبارت دیگر تابع را دنباله حقیقی میگویند هرگاه تابعی از مجموعه اعداد طبیعی به مجموعه اعداد حقیقی باشد به عبارت دیگر تابع را یک دنباله حقیقی میگویند. را یک دنباله حقیقی میگویند.
به عنوان مثال دنباله  دنبالهای حقیقی است چرا که برد آن از مجموعه اعداد حقیقی است. دنبالهای حقیقی است چرا که برد آن از مجموعه اعداد حقیقی است.
نمودار یک دنبالهاز آنجا که دنباله یک تابع با دامنه عداد طبیعی است میتوان دنباله را بوسیله نمودار نیز نمایش داد. این نمایش با دو روش انجام میشود. در یک روش میتوان مانند توابع دیگر آن را در دستگاه مختصات دکارتی رسم کرد و در روشی دیگر میتوان جملات آن را به همراه ذکر شماره آن جمله روی محور اعداد نشان داد. با ذکر یک مثال دو روش را توضیح میدهیم. به عنوان مثال میخواهیم دنباله اعداد زوج را به هر دو روش نشان دهیم:
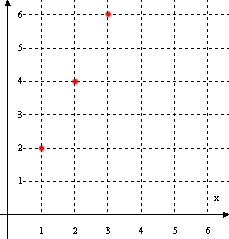
 جمله عمومی یک دنبالههمانطور که گفته شد یک دنباله تابعی با دامنه مجموعه اعداد طبیعی است پس برای دنباله ها در حالت کلی میتوان ضابطه تعیین کرد که به ضابطه یک دنباله جمله عمومی آن دنباله میگویند. جمله عمومی یک دنباله به منزله یک قانون است که بوسیله آن هر عضو از دامنه(مجموعه اعداد طبیعی) به یک عضو از مجموعه برد متناظر میشود و به ازای هر مقدار از متغیر n، جملات دنباله را تولید میکند. به عنوان مثال جمله عمومی دنباله اعداد طبیعی زوج به صورت  است که همانند ضابطه تابع بوسیله آن میتوان با قرار دادن هر n طبیعی جمله n ام است که همانند ضابطه تابع بوسیله آن میتوان با قرار دادن هر n طبیعی جمله n ام 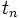 را بدست آورد. را بدست آورد.
البته لازم به ذکر است همه دنبالهها دارای جمله عمومی نمیباشند. به عنوان مثال تا کنون جمله عمومی برای دنباله اعداد اول تعیین نشده است. همچنین ممکن است یک سری از اعداد را به عنوان جملات دنباله انتخاب نمود که نتوان میان آنها رابطه ای برقرار نمود و جمله عمومی برای آنها نوشت. حال ممکن است این سوال پیش بیاید که آیا با در اختیار داشتن جملات یک دنباله می توان جمله عمومی آن را تعیین کرد؟ پاسخ را با یک مثال بررسی میکنیم. دنباله زیر را در نظر بگیرید:  میخواهیم جمله عمومی این دنباله را با توجه به جملاتش تعیین کنیم. با مشاهدهی جملات ممکن است حدس شما این باشد که این دنباله، دنباله اعداد طبیعی فرد بزرگتر از یک است و جمله عمومی آن را میتوان به این صورت نوشت:  اما این ممکن است یک جمله عمومی برای این دنباله باشد. ممکن است جملات دنباله در ادامه به این روال پیش نروند و جمله چهارم این دنباله عددی چون 9 نباشد! چرا که ما از جمله سوم به بعد دنباله هیچ اطلاعی نداریم و هر عدد دیگری نیز میتواند باشد! به عنوان مثال جمله عمومی دنباله فوق را میتوان به این صورت نوشت:  با نوشتن جملات این دنباله داریم:  مشاهده میکنید جملات این دنباله تا جمله سوم همانند دنباله  است ولی از جمله سوم به بعد مانند آن دنباله عمل نمی کند. است ولی از جمله سوم به بعد مانند آن دنباله عمل نمی کند.
پس همواره از روی جملات یک دنباله نمیتوان جمله عمومی آن را به درستی تعیین کرد. اما معمولاً برای نوشتن جمله عمومی یک دنباله با توجه به جملات آن، ساده ترین حالت را در نظر میگیریم. لذا جمله عمومی  برای این دنباله صحیحتر است و زودتر به ذهن خطور میکند. برای این دنباله صحیحتر است و زودتر به ذهن خطور میکند.
رابطه بازگشتی و دنباله بازگشتیبه دنباله اعداد زوج دقت کنید: ...,2,4,6,8,10,12 با کمی دقت در مییابید که برای بدست آوردن هر جمله کافی است جمله قبل را با عدد دو جمع کنید. به عنوان مثال برای بدست آوردن جمله پنجم(10) کافی است جمله چهارم(8) را با عدد دو جمع کنید. به این رابطه که بین جملات این دنباله برقرار است رابطه بازگشتی می گوییم.
به عنوان مثال دنباله فیبوناتچی دارای چنین رابطهای است که بوسیله آن مشخص میشود:  که جملات آن به این صورت است: ...,1,1,2,3,5,8,13,21 مشاهده میشود برای بدست آوردن هر جمله از جمله دوم به بعد کافی است دو جمله ماقبل آن جمله را با هم جمع کنیم. مثلا برای محاسبه جمله نهم داریم:  از آنجا که دنباله نیز تابع میباشد میتوان حد آن را نیز بررسی کرد که برای اطلاع از نحوه تعریف حد دنبالهها و محاسبه آنها میتوانید به مقاله حد دنباله رجوع کنید. منبع:رشد [ بازدید : 212 ] [ امتیاز : 3 ] [ نظر شما : ] [ دوشنبه 3 فروردين 1394 ] 12:42 ] [ امیرحسین جعفری ] [ ] حلقهحلقههرگاه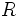 یک مجموعه ناتهی باشد ، گوییم مجموعه یک مجموعه ناتهی باشد ، گوییم مجموعه 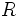 تحت دو عمل جمع و ضرب یک حلقه است ، هر گاه: تحت دو عمل جمع و ضرب یک حلقه است ، هر گاه:
حلقه جابجاییهرگاه حلقه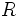 تحت عمل ضرب دارای خاصیت جابجایی باشد ، گوییم تحت عمل ضرب دارای خاصیت جابجایی باشد ، گوییم 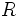 یک حلقه جابجایی(آبلی ) است. یک حلقه جابجایی(آبلی ) است.
مقسوم علیه صفرهرگاه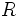 یک حلقه باشد ، عنصر یک حلقه باشد ، عنصر  را یک مقسوم علیه صفر نامند ، هرگاه عضوی مانند را یک مقسوم علیه صفر نامند ، هرگاه عضوی مانند  در حلقه در حلقه 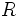 وجود داشته باشد ، بطوریکه وجود داشته باشد ، بطوریکه . .
در این تعریف اگر  ، آنگاه ، آنگاه 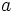 را مقسوم علیه چپ صفر مینامد و اگر را مقسوم علیه چپ صفر مینامد و اگر  ،آنگاه ،آنگاه 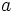 را مقسوم علیه راست صفر مینامند. را مقسوم علیه راست صفر مینامند.
واحد حلقهاگر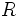 یک حلقه باشد،گوییم عنصری چون یک حلقه باشد،گوییم عنصری چون  ،یک حلقه(واحد حلقه) است،هرگاه ،یک حلقه(واحد حلقه) است،هرگاه 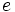 تحت عمل ضرب، عضو همانی باشد. یعنی: تحت عمل ضرب، عضو همانی باشد. یعنی:
 اگر حلقه ای دارای عنصر واحد باشد، گوییم حلقه یکدار است و این یک را با نماد  نشان میدهیم. نشان میدهیم.
حلقه بدیهیحلقه ای که فقط شامل عنصر صفر باشد، حلقه بدیهی نامیده میشود.نکتهاگر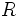 ، حلقه بدیهی باشد، یعنی ، حلقه بدیهی باشد، یعنی  ، آنگاه ، آنگاه  . .
قضیهاگر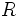 یک حلقه و یک حلقه و  باشند ،آنگاه گزاره های زیر برقرارند: باشند ،آنگاه گزاره های زیر برقرارند:
 1 1 2 2 3 3 4 4 5 5عنصر یکالهر گاه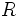 یک حلقه یکدار باشد، عنصر یک حلقه یکدار باشد، عنصر  را عنصر یکال مینامیم ، هرگاه را عنصر یکال مینامیم ، هرگاه 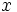 دارای وارون ضربی باشد .یعنی: دارای وارون ضربی باشد .یعنی:
 نکته
منبع:رشد [ بازدید : 561 ] [ امتیاز : 4 ] [ نظر شما : ] [ دوشنبه 3 فروردين 1394 ] 12:38 ] [ امیرحسین جعفری ] [ ] تابع
تعریف تابعدر ریاضیات تابع عملکردی است که برای هر ورودی داده شده یک خروجی منحصر بفرد تولید میکند معکوس این مطلب را در تعریف تابع بکار نمیبرند. یعنی در واقع یک تابع میتواند برای چند ورودی متمایز خروجیهای یکسان را نیز تولید کند. برای مثال با فرض y=x2 با ورودیهای 5- و 5 خروجی یکسان 25 را خواهیم داشت. در بیان ریاضی تابع رابطهای است که در آن عنصر اول به عنوان ورودی و عنصر دوم به عنوان خروجی تابع جفت شده است.به عنوان مثال تابع f(x)=x2 بیان میکند که ارزش تابع برابر است با مربع هر عددی مانند x
در واقع در ریاضیات رابطه را مجموعه جفتهای مراتب معرفی میکنند. با این شرط که هرگاه دو زوج با مولفههای اول یکسان در این رابطه موجود باشند آنگاه مولفههای دوم آنها نیز یکسان باشد. همچنین در این تعریف خروجی تابع را به عنوان مقدار تابع در آن نقطه مینامند. مفهوم تابع اساسی اکثر شاخههای ریاضی و علوم محاسباتی میباشد. همچنین در حالت کلی لزومی ندارد که ما بتوانیم فرم صریح یک تابع را به صورت جبری آلوگرافیکی و یا هر صورت دیگر نشان دهیم. فقط کافیست این مطلب را بدانیم که برای هر ورودی تنها یک خروجی ایجاد میشود در چنین حالتی تابع را میتوان به عنوان یک جعبه سیاه در نظر گرفت که برای هر ورودی یک خروجی تولید میکند. همچنین لزومی ندارد که ورودی یک تابع ، عدد و یا مجموعه باشد. یعنی ورودی تابع را میتوان هر چیزی دلخواه در نظر گرفت البته با توجه به تعریف تابع و این مطلبی است که ریاضیدانان در همه جا از آن بهره میبرند. تاریخچه تابعنظریه مدرن توابع ریاضی بوسیله ریاضیدان بزرگ لایب نیتر مطرح شد همچنین نمایش تابع بوسیله نمادهای (y=f(x توسط لئونارد اویلر در قرن 18 اختراع گردید، ولی نظریه ابتدایی توابع به عنوان عملکرهایی که برای هر ورودی یک خروجی تولید کند توسط جوزف فوریه بیان شد. برای مثال در آن زمان فوریه ثابت کرد که هر تابع ریاضی سری فوریه دارد.چیزی که ریاضیدانان ما قبل اوبه چنین موردی دست نیافته بودند، البته موضوع مهمی که قابل ذکر است آنست که نظریه توابع تا قبل از بوجود آمدن نظریه مجموعهها در قرن 19 پایه و اساس محکمی نداشت. بیان یک تابع اغلب برای مبتدیها با کمی ابهام همراه است، مثلا برای توابع کلمه x را به عنوان ورودی و y را به عنوان خروجی در نظر میگیرند ولی در بعضی جاها y,x را عوض میکنند. ورودی تابعورودی یک تابع را اغلب بوسیله x نمایش میدهند. ولی زمانی که ورودی تابع اعداد صحیح باشد. آنرا با x اگر زمان باشد آنرا با t ، و اگر عدد مختلط باشد آنرا با z نمایش میدهند. البته اینها مباحثی هستند که ریاضیدانان برای فهم اینکه تابع بر چه نوع اشیایی اثر میکند بکار میرود. واژه قدیمی آرگومان قبلا به جای ورودی بکار میرفت. همچنین خروجی یک تابع را اغلب با y نمایش میدهند در بیشتر موارد به جای f(x) , y گفته میشود. به جای خروجی تابع نیز کلمه مقدار تابع بکار میرود. خروجی تابع اغلب با y نمایش داده میشود. ولی به عنوان مثال زمانی که ورودی تابع اعداد مختلط باشد، خروجی آنرا با "W" نمایش میدهیم. (W = f(zتعریف روی مجموعههایک تابع رابطهای منحصر به فرد است که یک عضو از مجموعهای را با اعضای مجموعهای دیگر مرتبط میکند. تمام روابط موجود بین دو مجموعه نمیتواند یک تابع باشد برای روشن شدن موضوع ، مثالهایی در زیر ذکر میکنیم:
این رابطه یک تابع نیست چون در آن عنصر 3، با دو عنصر ارتباط دارد. که این با تعریف تابع متناقص است چون برای یک عنصر از مجموعه، دو عنصر در مجموعه موجود است
تعریف ساخت یافته تابعبطور ساخت یافته یک تابع از مجموعه x به مجموعه y بصورت f:x→y نوشته میشود و به صورت سه تایی مرتب ( (x,y,G(f) نمایش داده میشود. بطوری که (G(f زیر مجموعهای از حاصلضرب کارتزین xy میباشد. با این شرط که به ازای هر x در X یک Y متعلق به Y نسبت داد شود. با این شرط زوج مرتب (x,y) را در داخل (G(f میپذیریم. در این حالت نیز X را به عنوان دامنه f و y را به عنوان برد fو (G(f را به عنوان نمودار و یا گراف تابع F در نظر میگیرند.خواص توابعتوابع میتوانند:
توابع چند متغیرهیک تابع ممکن است بیشتر از یک متغیر داشته باشد برای مثال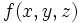 یک تابع از f است که دارای سه پارامتر x,y,z است که یک ارزش را برای تابع تولید میکنند. از توابع چند متغیره میتوان به قانون جاذبه نیوتن اشاره کرد که در آن دو جرم با متغیر یک تابع از f است که دارای سه پارامتر x,y,z است که یک ارزش را برای تابع تولید میکنند. از توابع چند متغیره میتوان به قانون جاذبه نیوتن اشاره کرد که در آن دو جرم با متغیر  و و 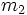 و نیز یک متغیر برای فاصله هر جرم به نام و نیز یک متغیر برای فاصله هر جرم به نام  در آن وجود دارد. در آن وجود دارد.
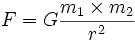 با مقدار دهی به سه پارامتر فوق مقدار تابع F محاسبه خواهد شد. منبع:رشد [ بازدید : 176 ] [ امتیاز : 3 ] [ نظر شما : ] [ دوشنبه 3 فروردين 1394 ] 12:35 ] [ امیرحسین جعفری ] [ ] عدد شادمجموع مربعات ارقام یک عدد صحیح چون  را را  تعریف می کنیم. به طریق مشابه مجموع مربعات ارقام عدد تعریف می کنیم. به طریق مشابه مجموع مربعات ارقام عدد  را را  تعریف میکنیم و به هین ترتیب. در انجام این عمل همواره در نهایت به یکی از این ده عدد خواهیم رسید: تعریف میکنیم و به هین ترتیب. در انجام این عمل همواره در نهایت به یکی از این ده عدد خواهیم رسید:
 اگر برای بعضی از i ها  باشد آنگاه عدد اولیه باشد آنگاه عدد اولیه  عدد مبارک،سعید یا شاد (Happy Number) گفته می شود. به عنوان مثال با شروع از عدد 7 دنباله زیر را بدست می آوریم: عدد مبارک،سعید یا شاد (Happy Number) گفته می شود. به عنوان مثال با شروع از عدد 7 دنباله زیر را بدست می آوریم:
 پس 7 عدد سعید یا شاد است.
 : :
تعداد جملات حاصل از هر یک از اعداد فوق تا زمانی که به عدد یک برسند به این صورت است: 

 به عبارت دیگر هر دو مولفه زوجهای زیر عدد سعید میباشند: 
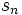 توانی از 10 نباشد(فرض خلف). پس توانی از 10 نباشد(فرض خلف). پس 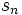 عددی m رقمی(m عددی طبیعی دلخواه است ) به صورت عددی m رقمی(m عددی طبیعی دلخواه است ) به صورت  است که است که  و برای هر و برای هر  طبیعی داریم طبیعی داریم  بنابه فرض چون جمله بعدی بنابه فرض چون جمله بعدی 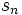
در دنباله عدد 1 است پس:  اما از طرفی چون اما از طرفی چون 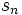 توانی از ده نمیباشد پس برای یک i که توانی از ده نمیباشد پس برای یک i که  خواهیم داشت خواهیم داشت  این نتیجه میدهد این نتیجه میدهد  که این ایجاب می کند که این ایجاب می کند  که این تناقض است. پس فرض خلف باطل و حکم ثابت می شود. که این تناقض است. پس فرض خلف باطل و حکم ثابت می شود.
با توجه به تعریفی که از عدد سعید ارائه شد واضح است که اگر  عددی سعید باشد هر یک از اعداد در دنباله عددی سعید باشد هر یک از اعداد در دنباله  نیز سعید خواهند بود. نیز سعید خواهند بود.
عددی که سعید نمیباشد عدد بد اقبال,نامبارک یا ناسعید (Unhappy Number) میگوییم. به عنوان مثال عدد شیطان یعنی عدد 666 عدد ناسعید است. چون اگر دنباله  را برای آن بنویسم خواهیم داشت: را برای آن بنویسم خواهیم داشت:
 مشاهده می شود عدد 37 در دنباله فوق دوبار تکرار شده است و همین مطلب
برای رد سعید بودن این عدد کافی است چون از اینجا به بعد سلسله جملات
37,58,89,145,42,20,4,16 در دنباله تکرار می شوند و این دنباله هیچ گاه به
یک نمیرسد. پس دنباله مربوط به اعداد ناسعید از جایی به بعد به صورت
متناوب تکرار می شود. همچنین همانند اعداد سعید در دنباله حاصل از اعداد
ناسعید همه منبع:رشد [ بازدید : 239 ] [ امتیاز : 3 ] [ نظر شما : ] [ دوشنبه 3 فروردين 1394 ] 1:27 ] [ امیرحسین جعفری ] [ ] هیپربولیک هیپربولیک [ بازدید : 191 ] [ امتیاز : 3 ] [ نظر شما : ] [ دوشنبه 3 فروردين 1394 ] 1:23 ] [ امیرحسین جعفری ] [ ] دكارت
رنه دکارت( Rene Decartes)، فیلسوف، ریاضیدان و فیزیکدان بزرگ عصر رنسانس در روز 31 ماه مارس 1596 میلادی، در شهرک لاهه از ایالت تورنِ(Touraine) فرانسه متولد شد. مادرش در سیزده ماهگی وی درگذشت و پدرش قاضی و مستشار پارلمان انگلستان بود. دکارت در سال 1606 میلادی، هنگامیکه پسر ده ساله ای بود، وارد مدرسه لافلش(La Fleche) شد. این مدرسه را فرقه ای از مسیحیان به نام ژزوئیتها یا یسوعیان تاسیس کرده بودند و در آن علوم جدید را همراه با تعالیم مسیحیت تدریس می کردند. دکارت طی هشت سال تحصیل در این مدرسه، ادبیات، منطق، اخلاق، ریاضیات و مابعدالطبیعه را فرا گرفت. در سال 1611 میلتدی، دکارت در یک جلسه سخنرانی تحت عنوان اکتشاف چند سیاره سرگردان در اطراف مشتری، از اکتشافات گالیله اطلاع حاصل کرد. این سخنرانی در روح او که تاثیر فراوان گذاشت. پس از اتمام دوره و خروج از لافلش، مدتی به تحصیل علم حقوق و پزشکی مشغول گردید، اما در نهایت تصمیم گرفت به جهانگردی پرداخته و آن گونه دانشی را که برای زندگی سودمند باشد، فرا بگیرد. به همین منظور، مدتی به خدمت ارتش هلند درآمد؛ چرا که فرماندهی آن را شاهزاده ای به نام موریس بر عهده داشت که در فنون جنگ و نیز فلسفه و علوم، مهارتی به سزا داشت و بسیاری از اشراف فرانسه دوست داشتند تحت فرمان او فنون رزمی را فرا بگیرند. دکارت در مدتی که در قشون ارتش هلند بود، به علم مورد علاقه خود، یعنی ریاضیات می پرداخت. در بهار سال 1619 میلادی از هلند به دانمارک و آلمان رفت و به خدمت سرداری به نام ماکسیمیلیان درآمد. اما زمستان فرا رسید و در دهکده نوبرگ(Neuberg) در حوالی رود دانوب، بی دغدغه خاطر و با فراغت تمام، به تحقیق در ریاضیات پرداخت و براهین تازه ای کشف کرد که بسیار مهم و بدیع بود و در پیشرفت ریاضیات، تاثیر به سزایی گذاشت. پس از مدتی، به فکر یکی ساختن همه علوم افتاد و در شب دهم نوابر 1619 سه رویای امید بخش دید و آن ها را چنین تعبیر کرد که: روح حقیقت او را برگزیده و از او خواسته تا همه دانش ها را به صورت علم واحدی در آورد. این رویاها به قدری او را مشعوف ساخت که نذر کرد تا مقبره حضرت مریم را در ایتالیا زیارت نماید. وی چهار سال بعد به نذر خود وفا کرد. از 1619 به بعد، چند سالی در اروپا به سیاحت پرداخت و چند سالی هم در پاریس اقامت کرد، اما زندگی در آن جا را که مزاحم فراغت خاطر خود می دید، نپسندید و در سال 1628 میلادی بار دیگر به هلند بازگشت و در آن دیار، تا سال 1649 میلادی، مجرد ، تنها و دور از هر گونه غوغای سیاسی و اجتماعی تمام اوقات خود را صرف پژوهش های علمی و فلسفی نمود. تحقیقات وی، بیشتر تجربه و تفکر شخصی بود و کمتر از کتاب استفاده می کرد. در سپتامبر 1649 به دعوت کریستین، ملکه سوئد برای تعلیم فلسفه خویش به دربار وی در استکهلم رفت. اما زمستان سرد این کشور اسکاندیناوی از یک سو و ضرورت سحرخیزی در ساعت پنج بامداد برای تعلیم ملکه از سوی دیگر، دکارت را که به این نوع آب و هوا و سحرخیزی عادت نداشت، به بیماری ذات الریه مبتلا ساخت. دکارت از دانشمندان و فیلسوفان بزرگ تاریخ به حساب می آید. او قانون شکست نور را در علم فیزیک کشف کرد و هندسه تحلیلی را در ریاضیات و هندسه بنا نهاد. در تاریخ فلسفه غرب ، فلسفه جدید با دکارت آغاز می کنند. برای اطلاعات بیشتر موارد زیر را ببینید: منابع
[ بازدید : 177 ] [ امتیاز : 3 ] [ نظر شما : ] [ دوشنبه 3 فروردين 1394 ] 0:57 ] [ امیرحسین جعفری ] [ ] مونثرمونژ
منبع :رشد [ دوشنبه 3 فروردين 1394 ] 21:50 ] [ امیرحسین جعفری ] [ ] |
|
|
[ طراح قالب : آوازک | Powered By : Avablog.ir | rss ] | ||