آموزش قدم به قدم ارنو روبیک (مکعب جادویی)
منبع:http://miniclub.blogfa.com/cat-48.aspx
[ بازدید : 172 ] [ امتیاز : 3 ] [ نظر شما : ]
[ چهارشنبه 27 اسفند 1393 ] 14:08 ] [ امیرحسین جعفری ]
[ ]
ریاضی خونهریاضی علم شیرین
|
آموزش قدم به قدم ارنو روبیک (مکعب جادویی)منبع:http://miniclub.blogfa.com/cat-48.aspx [ بازدید : 172 ] [ امتیاز : 3 ] [ نظر شما : ] [ چهارشنبه 27 اسفند 1393 ] 14:08 ] [ امیرحسین جعفری ] [ ] Terence Taoاین مقاله که شامل ترجمهی مصاحبهای کوتاه با Terence Tao است در بین فایلهای دوره تابستان یکی از سالهای پیش به چشم میخورد. چند خط از ابتدای این مقاله به این صورت است: Terence Tao (متولد آدلاید، استرلیا 1975) تنها 13 سال داشت که برنده مدال طلا در المپیاد جهانی ریاضی شد. در دو دورهی قبل از آن مدال برنز و مدال نقره گرفته بود. او درجه PHD خود را در سال 1996 از پرینستون گرفته و هم اکنون استاد تمام دانشگاه کالیفرنیا در لس آنجلس است و تا کنون جایزههای معتبری را نظیر Salem در سال 2000 و بنیاد Clay در سال 2003 دریافت کرده است. کارهای او در موضوعاتی نظیر آنالیز هارمونیک، معادلات دیفرانسیل با مشتقهای جزئی غیر خطی اثر داشته و مدال فیلدز را برای خدماتش در این زمینهها دریافت کرده. برای مطالعهی ادامهی این مقاله که شامل مصاحبهای با Tao است می توانید آن را از طریق لینک زیر دانلود کنید. منبعhttp://mathysc.com/content/%D9%85%D8%B5%D8%A7%D8%AD%D8%A8%D9%87-%D9%88-%D8%B2%D9%86%D8%AF%DA%AF%DB%8C%E2%80%8C%D9%86%D8%A7%D9%85%D9%87%E2%80%8C%D8%A7%DB%8C-%DA%A9%D9%88%D8%AA%D8%A7%D9%87-%D8%A7%D8%B2-terence-tao [ بازدید : 224 ] [ امتیاز : 4 ] [ نظر شما : ] [ چهارشنبه 27 اسفند 1393 ] 14:05 ] [ امیرحسین جعفری ] [ ] 11معادله ریاضی شگفت انگیز. معادله نسبیت عاممعادله بالا بخشی از توصیف نظریه نسبیت عام توسط آلبرت اینیشتین در سال 1915 میلادی است. این نظریه انقلابی را ایجاد کرد که سبب شد دنیای علم را با نحوه ارتباط مشخصه هندسی کائنات با فضا و زمان توضیح بدهد! ماریو لیویو منجم و ستاره شناس و اختر فیزیکدان برجسته موسسه علوم تلسکوپی در آمریکا بیان می کند: «قسمت سمت راست معادله انرژی کائنات را نشان می دهد (شامل انرژی ماده تاریک که نقش بسزایی در تعیین سرعت کهکشان ها دارد) و سمت چپ معادله بعد هندسی فضا-زمان را توصیف می کند. این معادله اینشتین ثابت می کند که جرم و ماده هندسه فضا را مشخص می کند و در نهایت چیزی را آشکار می سازد که ما آن را جاذبه می نامیم!» کایل کرانمر فیزیکدان دانشگاه نیویورک نیز می گوید: «با استفاده از این رابطه چرخش اجرام به دور اجرام سنگین تر و همچنین بسیاری دیگر از پدیده های نجومی و فیزیکی نظیر سیاهچاله ها را می توان اثبات نمود». 2. مدل استانداردیکی دیگر از معادلات بسیار مهم و بنیادی فیزیک معادله مدل استاندارد است که توصیف ذرات بنیادی جهان حاضر است. این معادله بر گرفته از یک معادله کلی تر به نام معادله استاندارد لاگرانژ (ریاضیدان و ستاره شناس قرن 18 فرانسه) است. لنس دیکسون متخصص برجسته شتاب دهنده کالیفرنیا می گوید: «این معادله به صورت موفقیت آمیزی تمامی ذرات بنیادین که تا کنون کشف شده اند نظیر ذره هیگز را بیان می کند اما تاکنون این معادله موفق نشده است که گرانش را توصیف نماید». معادله نسبیت خاص انیشتین بیان می دارد که مفاهیم فضا و زمان مفاهیمی مطلق نیستند بلکه به سرعت بیننده وابسته هستند  3. قضیه اساسی حسابدر حالی که 2 معادله پیشین در مورد ذرات تشکیل دهنده هستی بوده است اما معادله حساب ستون فقرات ریاضیات محسوب می شود که در خلاصه این محاسبات در 2 مفهوم انتگرال گیری و مشتق گیری خلاصه می گردد. قضیه اساسی حساب در قرن های اولیه بشریت نیز وجود داشته و پایه ریزی شده است اما در قرن 17 توسط نیوتن گسترش داده شد. وی از این قضیه برای توصیف حرکت سیارات به دور خورشید استفاده می کرده است.
 4. قضیه فیثاغورثمعادله «اودی یا گودی» که به قضیه فیثاغورث مشهور است. این قضیه می گوید که در مثلث قائم الزاویه مجذور وتر برابر است با مجموع مجذور اضلاع مجاور وتر! داینا تایمینا از دانشگاه کرنل می گوید که: این قضیه جزء اولین روابطی بود که من را بسیار شگفت زده کرد که چگونه می توان هندسه را با روابط ریاضیاتی ترکیب نمود!»
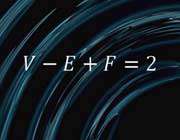 5. معادله اویلراین معادله به ظاهر ساده حقایق بسیار زیبایی را در مورد کره ها بیان می کند. کالین آدامز از کالج ویلیامز در ایالت ماساچوست می گوید: «این معادله بیان می دارد که اگر شما سطح یک کره را به یک چندوجهی تبدیل کنید به طوری کهF بیانگر تعداد وجه ها و E بیانگر تعداد لبه ها و V بیانگر تعداد رئوس باشد آنگاه همواره این معادله برقرار است: V-E+F=2 این رابطه برای هر نوع چندوجهی برقرار می باشد مانند هرم های 8 وجهی و غیره. حقیقت جالب این است که این معادله می تواند به ما اطلاعاتی در مورد ساختار اولیه کره ها قرار بدهد».  6.نسبیت خاصمعادله نسبیت خاص انیشتین بیان می دارد که مفاهیم فضا و زمان مفاهیمی مطلق نیستند بلکه به سرعت بیننده وابسته هستند. معادله بالا نشان می دهد که چگونه کاهش زمان یک رویداد با سرعت بیننده وابسته می باشد. بیل مورای از محققان برجسته شتاب دهنده سرن در ژنو می گوید: «برای یک دانشجوی قوی حل یک معادله سخت ریاضی و یا انتگرال های پیشرفته مهم نیست بلکه چیزی که مهم است نحوه نگاه کردن به پدیده های مختلف فیزیکی و ریاضیاتی و درک مفاهیم آن است و بتواند این مفاهیم را با جهان خارج ارتباط داد».  7. 0.99999999 = 1این معادله نماد این است که مقادیر مطلق در جهان وجود ندارد. این مطلق نبودن خود را در ساده ترین شکل و پایه ترین عدد یعنی 1 نشان می دهد که 1 برابر است با حد بینهایت 9 و مقدار مطلق 1 وجود ندارد!
 8.معادله اویلر لاگرانژ و قضیه نوترکرانمر از دانشگاه نیویورک می گوید: «این معادله هر چند خلاصه است اما مسایل بسیاری را نشان می دهد. این معادله انقلاب بزرگی را در مکانیک کوانتومی ایجاد کرده است. L در این معادله که اول کلمه لاگرانژ است پارامتری است که برای اندازه گیری انرژی سیستم به کار می رود. قضیه دیگری نیز در رابطه با این رابطه وجود دارد به نام قضیه نوتر که می گوید اگر شما در سیستم خود تقارن داشته باشید امکان ذخیره سازی انرژی بهتر وجود خواهد داشت. از این قانون در طراحی های مکانیکی و فضاپیماها استفاده می شود». 9.معادله کالان-سیمانزیکمعادله کالان سیمانزیک یک معادله بسیار حیاتی در فیزیک کوانتوم است. مت استراسلر فیزیکدان نظری دانشگاه راتجرس می گوید: «این معادله نشان می دهد که انتظارات ساده چقدر راحت در دنیای کوانتوم به شکست می انجامد! این معادله به فیزیکدانان بسیار کمک می کند که بتوانند اندازه جرم های کوانتومی نظیر پروتون و اندازه هسته را مشخص بکنند. معادله کالان سیمانزیک می تواند به ما نشان بدهد که نیروی گرانشی و الکتریکی بین 2 ماده با معکوس مجذور فاصله بین آن 2 متناسب می باشد. این معادله روابط بسیار پیچیده بین ذرات تشکیل دهنده نوترون ها و پروتون ها (کوارک ها) و نحوه نزدیک ماندن آنها با یکدیگر و در نتیجه تشکیل هسته را به ما توضیح می دهد. این معادله کاربردی بیشتر در ابعاد کوچکتر از پروتون و نوترون به کار می رود و می تواند اثرات ذرات در این ابعاد را برای محققان توصیف نماید». 10. معادله سطح حداقلفرانک مرگان از کالج ویلیامز می گوید: «این یک معادله غیر خطی است برای همین این معادله با معادلات خطی مشتقات جزیی مشهور نظیر معادلات گرما و معادله صوت و معادله شرودینگر در فیزیک کوانتوم در تضاد می باشد».
11. خط اویلرگلن ویتنی بنیانگذار موزه ریاضیات در نیویورک می گوید: «معادله ای که نام آن به نام کاشف آن لئونارد اویلر فیزیکدان و ریاضیدان قرن 18 سوییس نام گرفت بیان می دارد که اگر شما در هر مثلثی نقطه مرکز ثقل (نقطه ای که اگر شکل را بر روی یک سوزن قرار بدهیم آنگاه شکل به حال تعادل قرار می گیرد) و نقطه محل برخورد ارتفاع های هر یک از اضلاع و همچنین مرکز دایره محاطی مثلث را مشخص نمایید، همواره این 3 نقطه در حالت های مختلف بر روی یک خط به نام خط اویلر قرار دارد. این قضیه شگفتی ریاضیات را در توصیف الگوهای شگفت آور در اشکال ساده نمایش می دهد». منبع:http://www.tebyan.net/newindex.aspx?pid=270976    [ بازدید : 237 ] [ امتیاز : 3 ] [ نظر شما : ] [ چهارشنبه 27 اسفند 1393 ] 13:59 ] [ امیرحسین جعفری ] [ ] توان (فیزیک)توان (فیزیک)
از ویکیپدیا، دانشنامهٔ آزاد در فیزیک، توان میزان جابهجایی، دگرگونی و یا استفادهی انرژی در یکای زمان است. یکای این کمیت ژول بر ثانیه (J/s) یا همان وات است (به احترام جیمز وات، مخترع ماشین بخار). برای نمونه، برای یک لامپ، نرخ تبدیل انرژی الکتریکی به گرما و نور در وات شمرده میشود. هر چه لامپ پر توان تر باشد، انرژی الکتریکی بیشتری در یکای زمان تبدیل میشود. تبدیل انرژی را میتوان برای انجام کار استفاده کرد. پس توان همچنین نرخ انجام کار در یکای زمان است.
انتگرال توان روی زمان تعریف کار انجام شده است. چون این انتگرال به مسیر وارد کردن نیرو و گشتاور بستگی دارد، این محاسبه کار را "تابع مسیر" میخوانند. یکاهابعد توان انرژی بخش بر زمان است. یکای SI توان همان وات (W) است که برابر است با یک ژول بر ثانیه. از دیگر یکاهای توان میتوان ارگ بر ثانیه (erg/s)، اسب بخار (hp)، فوت-پوند بر دقیقه و یا یکای بریتانیایی حرارت بر ساعت (BTU/h) را خاطر نشان کرد. توان متوسطبه عنوان یک نمونه ساده، سوزاندن یک کیلوگرم زغال سنگ خیلی بیشتر از منفجر کردن یک کیلوگرم تیانتی انرژی آزاد میکند، ولی چون واکنش تیانتی سریعتر انرژی آزاد میکند توان خیلی بالاتر از زغالسنگ میرساند. اگر ΔW مقدار کار انجام شده در مدت زمان Δt باشد، آنگاه توان متوسط اینگونه تعریف میشود:
پس توان لحظهای مقدار حد توان متوسط است هنگامی که Δt به صفر میل میکند.
اگر توان P ثابت باشد، مقدار کار انجام شده در مدت زمان Τ اینگونه محاسبه میشود:
اگر انرژی تبدیل شده باشد، نماد E بیشتر از نماد W بکار میرود. توان مکانیکیتوان در سامانه های مکانیکی، آمیزشی از نیرو ها و حرکت است. به طور خاص، توان حاصلضرب نیروی وارد بر جسم در سرعت آن و یا حاصلضرب گشتاور اعمال شده بر یک محور و سرعت زاویهای آن است. توان مکانیکی نیز به صورت مشتق زمان کار تعریف میشود. درمکانیک، کار مکانیکی انجام داده شده توسط یک نیروی F بر روی جسمی که خم С را طی میکند را میتوان با انتگرال خطی زیر پیدا کرد:
به طوری که x متغیر مستقل خم C است و v سرعت در مسیر است. مشتق زمان این معادله، توان لحظه ای را میدهد:
در سامانه های چرخشی توان برابرست با حاصلضرب گشتاور τ و سرعت زاویهای ω.
در سامانه های سیال مانند محرک های هیدرولیکی (اَکتواتُر ها) توان برابرست با حاصلضرب فشار p به پاسکال (N/m2) در آهنگ شارش حجمی Q در متر مکعب بر ثانیه (m3/s):
مزیت مکانیکیاگر سامانه مکانیکی هیچ تلفاتی نداشته باشد، توان ورودی با توان خروجی برابر است. این اصل به ما فرمول سادهای برای مزیت مکانیکی سامانه میدهد. اگر توان ورودی سامانه، نیروی FA وارد بر نقطه ای با سرعت vA و توان خروجی سامانه نیروی FB وارد بر نقطه ای با سرعت vB باشد و هیچ تلفاتی در سامانه نداشته باشیم، آنگاه: و مزیت مکانیکی سامانه اینگونه بدست میآید:
روابط مشابهی برای سامانه های چرخشی موجودند: اگر توان ورودی سامانه دارای گشتاور TA و سرعت زاویهای ωA باشد و توان خروجی سامانه دارای گشتاور TB و سرعت زاویهای ωB باشد و سامانه هیچ تلفاتی نداشته باشد، آنگاه داریم:
و مزیت مکانیکی سامانه اینگونه بدست میآید:
این روابط برای تعریف کارایی بیشینه سیستم از لحاظ نسبت سرعت ها مفیدند. برای فهم بهتر اهمیت آنها این ویکی را بخوانید. توان در نورشناسیدر نورشناسی، یا رادیومتری، واژه توان گاهی به معنی شار تابشی است (نسبت متوسط جابهجایی انرژی توسط امواج الکترومغناطیسی که یکای آن وات است) و یا به توان دیوپتری یک عدسی یا آینه (مقیاسی از توانایی فوکوس کردن نور که یکای آن دیوپتر (m-1)است: P=1/f) اشاره دارد. توان الکتریکیتوان لحظهای الکتریکی ای که به مولفهای از مدار میرسد برابرست با:
به طوری که: اگر مولفه یک مقاومت است که نسبت ولتاژ به شدت جریان آن زمان-ناوردا است، آنگاه داریم:
به طوری که توان اوج و چرخه کار
در زنجیرهای از پالس های یکریخت، توان لحظه ای، تابعی متناوب از زمان
است. نسبت زمان پالس به دوره برابرست با نسبت توان متوسط به توان اوج که به
آن چرخه کار میگویند.
در مورد سیگنال متناوب
آنگاه توان متوسط اینگونه بدست میآید:
میتوانیم طول پالس τ را طوری تعریف کنیم که:
[ بازدید : 189 ] [ امتیاز : 3 ] [ نظر شما : ] [ چهارشنبه 27 اسفند 1393 ] 10:50 ] [ امیرحسین جعفری ] [ ] رادیکال تقریبی بدون استفاده از ماشین حساب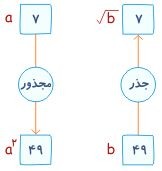 جذر به معنی ریشه ، بن و پایه است. در ریاضیات جذر گرفتن عکس عمل به توان رساندن میباشد.
عددهایی مانند ۴۹ , ۱۶ , ۴ , … را که جذر دقیق دارند ، مجذور یا مربع کامل مینامند. توجه: در دوره راهنمایی فقط جذر حسابی ( جذر مثبت) عدد a را در نظر میگیریم و آنرا با علامت نشان میدهیم. محاسبه مقدار جذر: ابتدا محاسبه مقدار تقریبی جذر اعداد در کلاس دوم را یاد آوری میکنیم: اگر a , b دو عدد مثبت باشند، جذر عددی مانند N از رابطه زیر بدست میآید: مثال: جذر عدد ۹۵ را تا یک رقم اعشار به دست آورید. برای محاسبه جذر یک عدد ، روش دقیقتری وجود دارد که به کمک این روش میتوانیم جذر یک عدد را تا هر تقریبی که بخواهیم ، حساب کنیم . پس از مطالعه چگونگی جذر از کتاب درسی ، جهت فراگیری بهتر به مثالهای زیر توجه کنید. مثال ۱: جذر عدد ۱۲۳۸ را با تقریب نقصانی کمتر از یک بدست آورید و باقیمانده را مشخص کنید. نکته: در محاسبه جذر تقریبی مقصود از تقریب نقصانی کمتر از یک این است که: حاصل جذر بدون رقم اعشاری محاسبه و بیان شود. در این صورت اختلاف جذر گرفته شده با جذر واقعی با دقت کمتر از یک واحد میباشد. مثال ۲: جذر عدد ۱۲۳۸ را تا یک رقم اعشار بدست آورید و باقیمانده را مشخص کنید. مثال ۳: جذر عدد ۲/۵۶ را تا دو رقم اعشاری بدست آورید و باقیمانده را مشخص کنید. امتحان جذر: اگر یک جذر را درست انجام داده باشیم: الف- دو برابر جذر به اضافه یک از باقیمانده ی جذر بزرگتر است. ب- مجذور جذر به اضافه باقیمانده ، مساوی عدد داده شده است. نکته: اگر بخواهیم جذر یک عدد اعشاری را امتحان کنیم، در مورد قسمت الف قبل از درج ممیزها، امتحان جذر را انجام میدهیم.
þ تست۱ : در یک عمل جذرگیری تقریبی از یک عدد، امتحان آن به صورت ۲۳<1+12×۲ شده است. آن عدد کدام گزینه میتواند باشد؟
حل : گزینه “د” صحیح میباشد. þ تست۲ : جذر مثبت حاصل ضرب دو عدد ۷۲ ×۵ ×۲۳ و ۱۱۲×۵۳×۲ برابر است با:
حل : گزینه الف صحیح میباشد. þ تست۳ : حل : گزینه ب صحیح است. þ تست۴ : در کدام گزینه همواره
حل : گزینه د صحیح است. عدد a منفی نیست، زیرا اعداد منفی جذر حقیقی ندارد. þ تست۵ : حل : گزینه ج صحیح است. þ تست۶ : در معادله توانی مقابل مقدار x کدام است
حل : گزینه ج صحیح است: منبع:http://netv.ir/%D9%86%D8%AD%D9%88%D9%87-%D9%85%D8%AD%D8%A7%D8%B3%D8%A8%D9%87-%D8%B1%D8%A7%D8%AF%DB%8C%DA%A9%D8%A7%D9%84-%D8%AC%D8%B0%D8%B1-%D8%A8%D8%AF%D9%88%D9%86-%D8%A7%D8%B3%D8%AA%D9%81%D8%A7%D8%AF%D9%87-%D8%A7/ [ بازدید : 382 ] [ امتیاز : 3 ] [ نظر شما : ] [ چهارشنبه 27 اسفند 1393 ] 10:43 ] [ امیرحسین جعفری ] [ ] انتگرالدر حساب دیفرانسیل و انتگرال ، از انتگرال یک تابع برای عمومیت دادن به محاسبه مساحت ، حجم ، جرم یک تابع استفاده می شود. فرایند پیدا کردن جواب انتگرال را انتگرال گیری گویند.البته تعاریف متعددی برای انتگرال گیری وجود دارد ولی در هر حال جواب مشابه ای از این تعاریف بدست می آید. انتگرال یک تابع مثبت پیوسته در بازه (a,b) در واقع پیدا کردن مساحت بین خطوط x=0 , x=10 و خم منفی F است . پس انتگرال F بین a و b در واقع مساحت زیر نمودار است. اولین بار لایب نیتس نماد استانداری برای انتگرال معرفی کرد و به عنوان مثال انتگرال f بین a و b رابه صورت 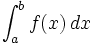 نشان می دهند علامت نشان می دهند علامت 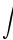 ،انتگرال گیری از تابع f را نشان می دهند ،aو b نقاط ابتدا و انتهای بازه
هستند و f تابعی انتگرال پذیر است و dx نمادی برای متغیر انتگرال گیری
است.
،انتگرال گیری از تابع f را نشان می دهند ،aو b نقاط ابتدا و انتهای بازه
هستند و f تابعی انتگرال پذیر است و dx نمادی برای متغیر انتگرال گیری
است.
از لحاظ تاریخی dx یک کمیت بی نهایت کوچک را نشان می دهد. هر چند در تئوریهای جدید، انتگرال گیری بر پایه متفاوتی پایه گذاری شده است به عنوان مثال تابع f را بین x=0 تا x=10 در نظر بگیرید ،مساحت زیر نمودار در واقع مساحت مستطیل خواهدبود که بین x=0 ،x=10 ،y=0 ،y=3 محصور شده است یعنی دارای طول 10 و عرض 3است پس مساحت آن برابر 30 خواهد بود . اگر تابعی دارای انتگرال باشد به آن انتگرال پذیر گویند و تابعی که از انتگرال گیری از یک تابع حاصل می شود تابع اولیه گویند . اگر انتگرال گیری از تابع در یک محدوده خاص باشند به آن انتگرال معین گویند که نتیجه آن یک عدد است ولی اگر محدوده آن مشخص نباشد به آن انتگرال نامعین گویند. محاسبه انتگرالاکثر روش های اساسی حل انتگرال بر پایه قضیه اساسی حساب دیفرانسیل و انتگرال بنا نهاده شده است که بر طبق آن داریم: 1.f تابعی در بازه (a,b) در نظر می گیریم . 2.پاد مشتق f را پیدا می کنیم که تابعی است مانند f که و داریم: 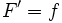
3.قضیه اساسی حساب دیفرانسیل و انتگرال را در نظر می گیریم: 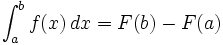
بنابراین مقدار انتگرال ما برابر 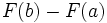 خواهد بود. خواهد بود.
به این نکته توجه کنید که انتگرال واقعاً پاد مشتق نیست (یک عدد است) اما قضیه اساسی به ما اجازه می دهد تا از پاد مشتق برای محاسبه مقدار انتگرال استفاده کنیم . معمولاً پیدا کردن پاد مشتق تابع f کار ساده ای نیست و نیاز به استفاده از تکنیکهای انتگرالگیری دارد این تکنیکها عبارتند از :
روش هایی دیگر نیز وجود دارد که برای محاسبه انتگرالهای معین به کار می رود همچنین می توان بعضی از انتگرال ها با ترفند هایی حل کرد برای مثال می توانید به انتگرال گاوسی مراجعه کنید . تقریب انتگرالهای معین
انتگرال هایی معین ممکن است با استفاده از روش های انتگرال گیری عددی ،تخمین زده شوند.یکی از عمومی ترین روش ها ،روش مستطیلی نامیده می شود در این روش ناحیه زیر نمودار تابع به یک سری مستطیل تبدیل شده و جمع مساحت آنها نشان دهنده مقدار تقریبی انتگرال است. از دیگر روش هایی معروف برای تخمین مقدار انتگرال روش سیمپسون و روش ذوزنقه ای است. اگر چه روش های عددی مقدار دقیق انتگرال را به ما نمی دهند ولی در بعضی از مواقع که انتگرال تابعی قابل حل نیست یا حل آن مشکل است کمک زیادی به ما می کند . تعریف های انتگرالاز مهم ترین تعاریف در انتگرال می توان از انتگرال ریمان و انتگرال لبسکی(lebesgue) است. انتگرال ریمان بوسیله برنهارد ریمان در سال 1854 ارئه شد که تعریف دقیقی را از انتگرال ارائه می داد تعریف دیگر را هنری لبسکی ارائه داد که طبق این تعریف شرایط تعویض پذیری حد و انتگرال با شرط مساوی ماندن عبارت، ارائه می کرد. از دیگر تعاریف ارائه شده در زمینه انتگرال میتوان به انتگرال riemann-stieltjes اشاره کرد. پس به طور خلاصه سه تعریف زیر از مهمترین تعاریف انتگرال میباشند: سایتهای مرتبطمحاسبه آنلاین انتگرال جدول انتگرالها پیوندهای خارجیhttp://en.wikipedia.org/wiki/Integral منبع:رشد [ بازدید : 211 ] [ امتیاز : 3 ] [ نظر شما : ] [ چهارشنبه 27 اسفند 1393 ] 10:37 ] [ امیرحسین جعفری ] [ ] اصل کاوالیریبوتاون تورا کاوالیری (1564-1642) اهل میلان، از همان سال های نخستین به ریاضیات علاقه مند بود،و به ظاهر زیر تاثیر گالیله، روش « غیر قابل تقسیم ها» را در هندسه بوجود آورد که در اثر بزرگ او در سال 1635، با عنوان «هندسه، با طرح تازه ای بر اساس غیر قابل تقسیم های پیوسته»، به شهرت رسید. غیر قابل تقسیم ها، از نظر کاوالیری، وترهای موازی در درون شکل روی صفحه، و صفحه های موازی در درون جسم بود. او برای مقایسه ی شکل های روی صفحه و جسم های فضایی، مفهوم « مجموع همه ی غیر قابل تقسیم ها» را آورد که تماس سطح و فضای جسم را پر می کردند. برای کاوالیری، نسبت این مجموع ها، همان نسبت مساحت ها و حجم ها بود. او شکل های روی صفحه را، بین دو خط راست موازی در نظر گرفت. اصل کاوالیری درباره مساحت: اگر فرض کنیم قاعده های دو شکل بر روی یک خط قرار گرفته باشند. اگر هر خطی موازی قاعده های دو شکل در آنها قطعه هایی با طول های مساوی ایجاد کند، مساحت های آن دو شکل برابر است. با توجه به شکل دو شکل بر روی افق قرار گرفته اند. اگرهر خطی به موازات قاعده مانند d رسم کنیم و داشته باشیم: AB=CD، MN=PE ، آنگاه دو شکل هم مساحت هستند.
اصل کاوالیری در باره حجم ها: دو شکل فضایی و صفحه ای که قاعده های دو شکل در آن قرار گرفته باشد را نظر بگیرید. اگر هر صفحه ای موازی با این صفحه که یکی از این دو شکل را قطع می کند، دیگری را نیز قطع می کند و سطح مقطع های حاصل دارای مساحت های برابر باشند، آنگاه این دو شکل فضایی حجم یکسان دارند. خود کاوالیری در این زمینه می نویسد: «دو جسمی که قاعده ی آنهای بر یک صفحه و ارتفاعشان برابر باشد، به شرطی هم ارزند یعنی حجم های برابر دارند که مقطع های آنهابا صفحه های موازی با قاعده باشد.» این نظام کار، به نام «نظام کاوالیری» معروف است. کاوالیری بر پایه ی این نظام، قضیه های زیادی را اثبات می کند. برای نمونه، ثابت کرد نسبت مساحت های دو مثلث متشابه برابر است با نسبت مجذور ضلع های متناظر آن ها. ابهامی که در مفهوم «مجموع غیر قابل تقسیم ها» وجود دارد، موجب اعتراض و انتقاد سخت بعضی از هم عصران کاوالیری شد. به همین خاطر کاوالیری کتاب دیگری با نام «شش طرح هندسی» را نوشت که در آن، تلاش کرد مفهوم هایی را که بکار می برد، دقیق تر کند، با وجود این، خود کاوالیری تا پایان زندگی نسبت به کافی بودن استدلالهای خود در تردید باقی بود، گرچه به درستی آن ها اعتقاد داشت. طرح کاوالیری در هندسه و آموزش او درباره ی غیر قابل تقسیم ها، تنها برای درک بهتر هندسه ی مقدماتی سودمند نبود. این آموزش، یعنی جمع کردن غیر قابل تقسیم ها، پیش در آمدی برای انتگرال گیری بود. کاوالیری نماد انتگرال را بکار نمی برد، ولی در واقع از انتگرال گیری استفاده می کرد... به جز این، در هندسه ی کاولیری به قضیه هایی بر می خوریم که برای پیدایش محاسبه ی دیفرانسیلی، ارزش معینی دارند. از آن جمله، نخستین گزاره ای که در هندسه آمده، هم ارز با قضیه رول است، و به دنبال آن گزاره ای آمده است که مضمون آن اینست: در نقطه های ماکزیمم و می نیمم تابع، مماس بر نمودار با محور طول ها موازی است. یکی از کمبود های جدی هندسه ی کاوالیری این است که مولف از بکارگیری جبر فراری است و همه جا به هندسه دانان قدیمی تکیه می کند. بی تردید، بکار گیری نمادهای جبری که در زمان کاوالیری رایج شده بود، می توانست کارهای او را دقیق تر، کامل تر و قابل درک تر کند.
منبع:http://www.reyazi.blogfa.com/post-34.aspx  [ بازدید : 295 ] [ امتیاز : 3 ] [ نظر شما : ] [ چهارشنبه 27 اسفند 1393 ] 10:24 ] [ امیرحسین جعفری ] [ ] |
||
|
[ طراح قالب : آوازک | Powered By : Avablog.ir | rss ] | |||